JamieJQuinn Research Software Engineer
Parallelising Wondrous Numbers in C++
The Collatz conjecture, named for Lothar Collatz, goes as follows.
Take any positive integer \(n\). If \(n\) is even, half it, or if it’s odd, multiply it by three and add one. Repeating the process will always bring you back to 1.
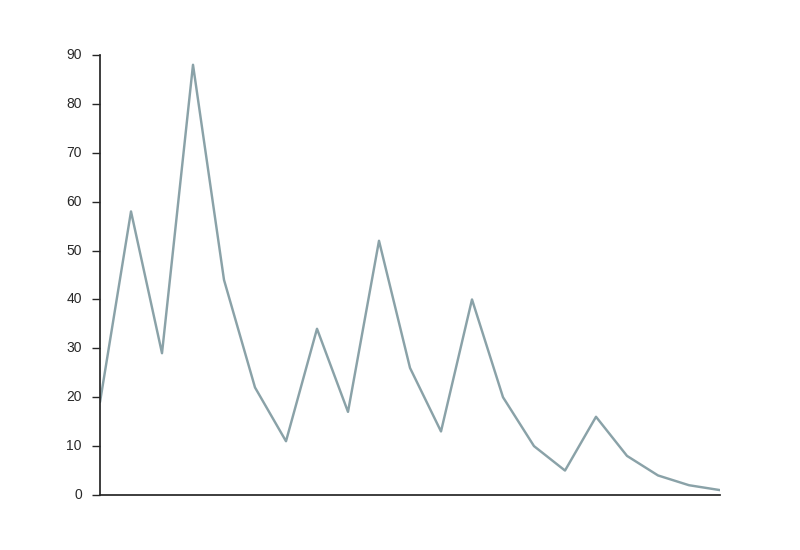
The sequence of numbers generated by repeating the process is sometimes called the hailstone sequence due to the strange way the sequence bounces around, as you can see below if we start the sequence at 19. The numbers generated are also called the wondrous numbers, a name I found so enticing that I named this post for it.
This problem is deceptively simple, isn’t it? You can definitely see that ever power of 2 must come back to 1, that’s pretty easy to see after playing about with the process for a while. It’s this deceptive simplicity of the problem that really makes it a kind of mathematical disease, so well described in the xkcd comic below.

It’s almost infuriating that this seemingly straightforward problem hasn’t been solved, but check out some of the complex maths needed to even try and think about proving this at Terry Tao’s blog.
Stopping Times
Fortunately I didn’t catch the disease of obsessively trying to prove this. I did however become slightly obsessed with the stopping times of the sequences. Simply put, the stopping time is how many numbers does the process have to go through before you get back to 1. For example, 1 has a stopping time of 0, since it’s already at 1, and any powers of 2 will have a stopping time of precisely the power. We can count the stopping time of the hailstone sequence above to be about 20, depending on if you’re counting 19 and/or 1 in the steps. Calculating each of the stopping times for numbers up to ten thousand gives a fascinating pattern, as you can see below.
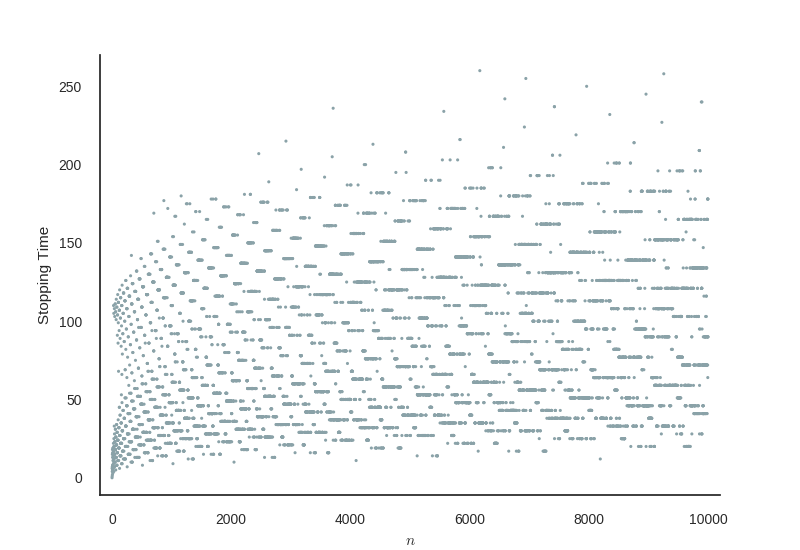
So this pattern is nice but what makes the calculation of all these stopping times so lovely is that it’s an example of an pleasingly parallel problem, that is a problem that’s so easy to split up and solve in parallel that it’s just satisfying in its simplicity. Calculating the stopping time for one number doesn’t depend at all on the calculation of another, hence we can split the domain up very simply and calculate each one independently in whichever way we choose. What better to introduce myself to the various methods of parallel programming, specifically in C++?
The problem I put forth was simply this:
What is the longest stopping time possible (for integers below some limit)?
Just looking at the stopping times graphed above, you can see that the number with the longest stopping time under 10000 is about 6250 or so, having a stopping time of about 260.
Finding the maximum stopping time gives a nice number that can be used to test and verify results from different implementations of the solution, but we still have to calculate (almost) every single stopping time. That “almost” appears because if you consider a hailstone sequence starting from \(n\), every other number in that sequence must have a lower stopping time than \(n\), since that sequence is entirely inside the sequence starting from \(n\). That means that once we’ve calculated the stopping time for some number \(n\), we can forget about all the numbers in \(n\)’s hailstone sequence. However, even though taking advantage of this could theoretically speed up the solution of the problem, the mere act of taking numbers out of the domain takes some computation time so it’s not obvious whether a speed up would actually be gained. I may experiment with this but that’s a topic for another post.
The Serial Solution
You’ll find all the code, scripts and bits and pieces on my github.
Although many simulations shouldn’t be built serially and then parallelised, since this is a pleasingly parallel problem, it shouldn’t be an issue, so let’s think about solving this in a serial fashion first. We can code a function that finds the path length for a given starting number as follows.
int calcCollatzPathLength(big_int n) {
int pathLength=0;
while(n>1) {
if(n%2 == 1) {
n=n*3+1;
} else {
n/=2;
}
++pathLength;
}
return pathLength;
}
You’ll find in the actual code the definition of big_int as a typedef defining whatever we’re considering to be a large integer (I usually used 64-bit integers, i.e. long long) and also some little bits that catch overflow problems. I specifically chose to simply ignore those sequences that overflowed for ease of programming, of course it does mean we might miss the true maximum path length but I’m fine with that. Total accuracy is not the main point of this whole exercise.
Another point to make is that this could have been implemented recursively instead of using a while loop, and it might be interesting to compare the efficiency of the loop against recursion, however GPU core typically don’t use stacktraces, can’t call functions and thus can’t use recursive techniques. For simplicity I just stuck to the while loop.
To find the maximum, we apply our calcCollatzStoppingTime function over the range of integers we’re interested in.
void maxCollatzPath(
big_int N,
big_int M,
// Return values
int &maxStoppingTime,
big_int &maxN
) {
maxStoppingTime=0;
maxN=0;
for(big_int i = N; i<M; ++i) {
int stoppingTime = calcCollatzStoppingTime(i);
if ( maxStoppingTime < stoppingTime ) {
maxStoppingTime=stoppingTime;
maxN=i;
}
}
}
And that’s basically that…
OpenMP (aka the lazy man’s multithreading)
OpenMP is wonderful. By simply installing the libraries and adding the appropriate compiler directive your code is instantly multithreaded. So all we need to do to allow openMP to do it’s thing in our code is add the parallel for directive just before the for loop in our serial implementation, as you can see below. What an absolute belter.
#pragma omp parallel for schedule(dynamic)
for(big_int i = N; i<M; ++i) {
int stoppingTime = calcCollatzStoppingTime(i);
if ( maxStoppingTime < stoppingTime ) {
maxStoppingTime=stoppingTime;
maxN=i;
}
}
You can find more about openMP in general from this wonderful tutorial, but in short, the pragma shown above simply tells openMP to create a bunch of threads specifically to handle the for loop and dole out the inputs using the dynamic schedule which allows better distribution of the work.
C++ Threads
Originally this was threaded using boost threads, but since C++11 the language has had its own implementation of threads, modelled on boosts implementation. The implementation is simple, create a number of threads and give each of those threads en equal portion of the work. You can see the implementation in C++11 thread parlance below.
void threadedCollatz() {
int stoppingTimes[N_THREADS];
big_int maxNs[N_THREADS];
big_int nPerThread = big_int(upperLimit/N_THREADS);
// Create and run threads
std::thread threads[N_THREADS];
for(int i=0; i<N_THREADS; ++i) {
threads[i] = std::thread(maxCollatzPath, i*nPerThread, (i+1)*nPerThread,
std::ref(stoppingTimes[i]), std::ref(maxNs[i]));
}
// Get max out of all thread return values
int maxStoppingTime = 0;
big_int maxN = 0;
for(int i=0; i<N_THREADS; ++i) {
threads[i].join();
if(stoppingTimes[i] > maxStoppingTime) {
maxStoppingTime = stoppingTimes[i];
maxN = maxNs[i];
}
}
printMax(maxStoppingTime, maxN);
}
Thinking about the problem for a little while, you might think to say something along the lines of,
Ahh, but Jamie, won’t the numbers that have the longest stopping time cluster around the top end? Thus, the thread that receives the last block of numbers will inevitably run much slower than the others.
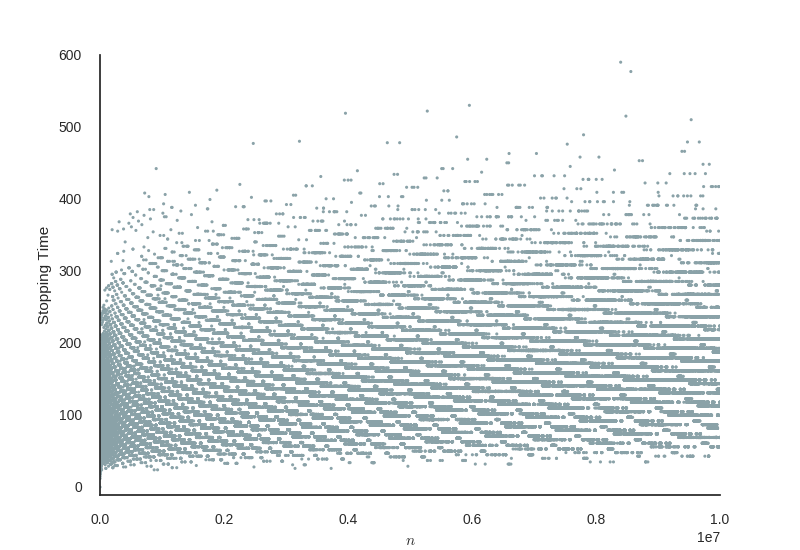
It’s perfectly plausible, but then I tried interlacing the numbers given to the threads, even giving them random numbers, and it just didn’t seem to help much. Looking at a sample of the stopping times below, for numbers up to 10,000,000, you can actually see that the stopping times are pretty well dispersed anyway, we absolutely should see little speed up, if any at all, if we interlace things, it’s going to give the same result!
OpenCL with Boost Compute
This was the fun one. I’d never done much GPU programming before so when I actually managed to get it to work I was so elated I had to take a wee break and eat a digestive. The code is remarkably simple thanks to the Boost compute library.
The code that actually runs on each of the GPU cores is identical to the serial version, but we wrap it in the BOOST_COMPUTE_FUNCTION macro to let Boost convert it properly. Note the use of cl_ulong, the equivalent to our previously used long long.
BOOST_COMPUTE_FUNCTION(int, gpu_calc_stopping_time, (cl_ulong n), {
/* SERIAL CODE */
});
Then, we set up the device, load the starting numbers into the GPU and tell it to compute the stopping time for each one using the transform function, similar to a functional map. Then we find the maximum stopping time (still on the GPU) and return the value. It’s a little bit of boilerplate code to copy data to and from the GPU and this is a very rough implementation, but I just find this code amazingly simple.
void boostCompute() {
// Setup device
compute::device device = compute::system::default_device();
compute::context context(device);
compute::command_queue queue(context, device);
// Fill array with increasing values
std::vector<cl_ulong> starting_points(UPPER_LIMIT);
for(int i=0; i<UPPER_LIMIT; ++i) {
starting_points[i] = i+1;
}
// Copy numbers over
compute::vector<cl_ulong> device_vector(UPPER_LIMIT, context);
compute::copy(
starting_points.begin(), starting_points.end(), device_vector.begin(), queue
);
// Calculate stopping time on each value
compute::transform(
device_vector.begin(),
device_vector.end(),
device_vector.begin(),
gpu_calc_stopping_time,
queue
);
// Find max
compute::vector<cl_ulong>::iterator max =
compute::max_element(device_vector.begin(), device_vector.end(), queue);
// Get max back
compute::copy(max, max + 1, starting_points.begin(), queue);
int maxStoppingTime = starting_points[0];
int maxN = max - device_vector.begin() + 1;
printMax(maxStoppingTime, maxN);
}
The Benchmark
Running a little benchmarking script that times each implementation running ten times each to get an average, we compare the parallel implementations with the serial version.
| Serial | OpenMP | Threaded | Boost Compute | |
|---|---|---|---|---|
| Average Time | 5.306 | 1.620 | 1.595 | 0.214 |
| Speedup | 1 | 3.27 | 3.33 | 24.79 |
This benchmark was performed on an Intel i5 quad core processor, with the GPU code running on an Nvidia GTX 570 (about 450 cores).
Conclusion
This blog post is a few things, a comparison of parallel methods, an example of a nice pleasingly parallel mathematics problem, and just a log of my introduction to parallel programming in general. To conclude the comparison of the methods, the wonderful speed up of between 3 and 4 times from the openMP and threading implementations is to be expected on a quad core machine. What is really quite important to note is, at least for this simple parallel problem, openMP was realistically just as effective at speeding up the code as the handwritten threading stuff, but openMP is just one line of code. That’s just amazing. With just a little bit more work, the speedup from implementing this on the GPU is undoubtedly worth it in this case. 25 times faster is just crazy, especially on a 5-6 year old graphics card.
Please do send me any feedback you have on this, be it about the maths, the code or even just the writing. This blog and my writing style are still in infancy so any feedback at all is incredibly helpful. Cheers for reading!
Written on February 14th, 2017 by Jamie QuinnHeader image credits - u/level1807